Lernziele
Lernziele
Nach der Bearbeitung dieses Unterkapitels sollen Sie in der Lage sein,
- die drei Definitionen der Elektronegativität zu beschreiben,
- das Konzept der Partialladung zu erläutern,
- Qualitativ das Dipol einer Bindung vorhersagen,
- den begriff Polarität erklären
- den Begriff "ionischen Bindungsanteil" erklären und Methoden zu dessen Bestimmung zu benennen,
- und die Elektronenzahl eines Atoms in Bezug auf Oktettregel, sowie dessen formale Ladung und Oxidationszahl zu bestimmen.
Auf der nächsten Seite findet Ihr eine Einführung zum Thema Elektronegativität.
Elektronegativität
Die Elektronegativität (EN) beschreibt die Fähigkeit eines Atoms, welches sich in einer kovalenten Bindung befindet, das bindende Elektronenpaar stärker an sich zu binden als es der Bindungspartner vermag. Das Elektronenpaar hält sich im zeitlichen Mittel demzufolge näher an diesem Atom auf als an seinem Bindungspartner.
Es existieren unterschiedliche Elektronegativitätsskalen in Abhängigkeit davon, wie die Elektronegativität formal definiert und experimentell bestimmt wird.

Pauling
Bildquelle
Die erste Elektronegativitätsskala stammt von Pauling. Pauling erkannte, dass eine Bindung zwischen zwei Atomen mit verschiedenen EN dazu führt, dass beide Atome eine Ladung tragen. Dies führt dazu, das die beiden Atome nicht nur durch die kovalente Bindung zusammengehalten werden, sondern dass es zusätzlich anziehende ionische Wecxhselwirkungen gibt. Laut Pauling ist die Elektronegativitätsdifferenz (χA - χB) zweier Atome ein Maß für den ionischen Anteil der Bindung zwischen diesen Atomen. Sie wird mithilfe der Dissoziationsenergien DAA, DBB und DAB, die für die Moleküle A-A, B-B und A-B ermittelt wurden, bestimmt.
\[ \left( \chi_A - \chi_B \right)^2 = \frac{D_{AB} - \sqrt{D_{AA} * D_{BB}}}{96,48 \frac{kJ}{mol}} \]Dieser Ausdruck wirkt erst einmal recht komplex. Daher soll die Gleichung systematisch diskutiert werden.
- Im Zähler rechts findet sich der Ausdruck \( \sqrt{D_{AA} * D_{BB}} \). Dieser Wert ist das geometrische Mittel von DAA und DBB. Meistens wird bei Berechnungen nicht das geometrische Mittel, sondern das arithmetische Mittel \( \frac{D_{AA} + D_{BB}}{2} \) benutzt. Pauling nutzt hier aus guten Gründen (später mehr) das geometrische Mittel.
-
Dieser Mittelwert liefert eine gute Vorhersage für die Stärke
der kovalenten Bindung zwischen A und B. DAB ist die
tatsächliche Stärke der Bindung zwischen A und B. Die Differenz
\( D_{AB} - \sqrt{D_{AA} * D_{BB}} \) liefert also den Unterschied zwischen
beobachteter Bindungsstärke und vorhergesagter Stärke der
kovalenten Bindung zwischen A und B.
Diese Differenz entspricht nun dem Anteil der Bindung, der nicht auf kovalenten Bindungen sondern auf ionischen Wechselwirkungen beruht. - Eine solche Betrachtung liefert keine EN für jedes Atom, sondern nur eine EN-Differenz für zwei Atome.
-
Betrachtet man nun drei Atome, so ergibt sich ein Problem: Man kann mit Hilfe
der Dissoziationsenergien DAA, DBB, DCC,
DAB und DAC die EN-Differenzen χAB und
χAC berechnen.
Im nächsten Schritt kann man dann auch χBC berechnen. Dazu gibt es jetzt zwei Möglichkeiten:
(i) Wir bilden die Differenz χBC = χAC - χAB,
oder
(ii) wir berechnen die Differenz χBC mit Hilfe von DAC nach obiger Gleichung.
-
Dabei erhalten wir nicht automatisch den gleichen Wert.
Um ein (im Rahmen der Messgenauigkeit) selbstkonsistentes System
zu erhalten sind gewisse Maßnahmen notwendig.
- Die Differenz \( \chi_A - \chi_B \) wird quadriert.
- Es wird das geometrische Mittel anstelle des arithmetischen Mittels verwendet.
- Die Division durch \( 96,48 \frac{kJ}{mol} \) dient einer Normierung. So werden in der zweiten Periode EN von 1 (Li) bis 4 (F) erhalten. Die EN nimmt im Periodensystem von links nach rechts zu und von oben nach unten ab.
Auf der nächsten Seite findet Ihr weitere Methoden zur Beschreibung der EN.
Elektronegativität
Wie zuvor schon erläutert, existieren unterschiedliche Elektronegativitätsskalen.

Mulliken
Bildquelle
Laut Mulliken ist die Elektronegativität (χ) der Mittelwert aus Ionisierungsenergie (EI) und Elektronenaffinität (EEa):
\[ \chi = \frac{E_I + E_{Ea}}{2} \]Dies stellt die Betrachtung auf eine mehr physikalische Ebene . Darüberhinaus erlaubt diese Betrachtung die Bestimmung absoluter EN. Diese Skala hat aber fast keine Bedeutung. Es gibt aber auch eine modifizierte Skala nach Mulliken. Hier erechnet sich Χ nach:
\[ \chi = 1.35 \sqrt{\frac{E_I + E_{Ea}}{2}} - 1,37 \]Diese Gleichung wirkt wieder komplex, hat aber einen großen Vorteil. Sie enthält letztlich nur eine Normierung und mit dieser Normierung werden die Werte den Werten von Pauling sehr ähnlich.
Eine dritte Skala stammt von Allred und Rochow. Sie definieren die Elektronegativität als die Coulomb-Kraft (F), welche die, von inneren Elektronen abgeschirmte, Kernladung (Zeff) auf die Bindungselektronen ausübt:
e = Elementarladung
r = Abstand von Elektron und Kern
ε0 = Dielektrizitätskonstante des Vakuums
\[ \chi = \frac{e^2 Z_{eff}}{4 \pi \epsilon_0 r^2} \] Durch eine einfache Skallierung ist es möglich, auch diese Skala an die Pauling-Skala anzupassen: \[ \chi = \frac{3590 Z_{eff}}{r^2} + 0,744 \]Heute werden alle drei Skalen in die an die an Pauling adaptierten Versionen verwendet. Die Unterschiede sind gering und für die meisten belange spielt die Wahl der Skala keine Rolle.
Auf der nächsten Seite wird der Begriff Partialladung erläutert.
Partialladungen
Sobald ein Molekül nicht mehr ausschließlich aus homonuklearen Atomen besteht (z.B. H2, Cl2) sondern auch kovalente Bindungen zwischen Heteroatomen vorliegen (z.B. HCl, CO2) werden aufgrund der Elektronegativitätsdifferenz zwischen den Atomen, die bindenden Elektronen vom elektronegativeren Bindungspartner stärker angezogen. Daraus resultiert eine ungleichmäßige Elektronen- und damit Ladungsverteilung zwischen den Bindungspartnern. Diese führt zu sogenannten Partialladungen. Das elektronegativere Atom der kovalenten Bindung weist eine etwas höhere negative Ladung bzw. Elektronendichte als im atomaren bzw. homonuklear gebundenen Zustand auf. Es ist partiell negativ geladen. Das weniger elektronegative, sprich elektropositivere Atom der kovalenten Bindung weist eine etwas geringere negative Ladung bzw. Elektronendichte als im atomaren bzw. homonuklear gebundenen Zustand auf. Es ist partiell positiv geladen. Liegt ein solcher Fall vor, hat die betrachtete Bindung eine gewisse Polarität. In der Lewis-Struktur wird die Partialladung, ebenso wie die Formalladung, hinter dem Elementsymbol des Atoms hochgestellt angeführt. Sie besteht aus dem Vorzeichen der Ladung, dem der griechische Kleinbuchstabe δ vorangestellt wird. Somit ist sie eindeutig von der Formalladung zu unterscheiden.
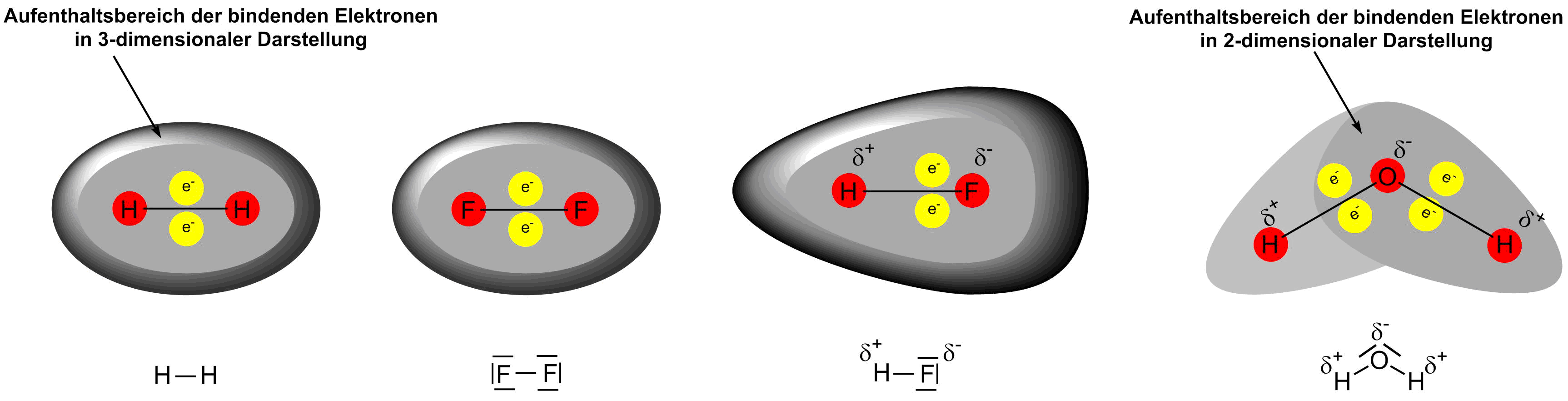
Elektronenverteilung unpolarer und polarer Verbindungen
Auf der nächsten Seite wird der Begriff Dipol eingeführt.
Polarität und Dipolmoment
Ein Maß für die Polarität einer Bindung ist ihr Dipolmoment (μ). Das Dipolmoment (μ) ist definiert als:
μ = q ∗ d
q ist eine Ladung, d ist der Abstand zwischen zwei Ladungen entgegengesetzter Vorzeichen
Befinden sich zwei Punktladungen gleichen Betrags aber entgegengesetzter Vorzeichen in einem Anstand d voneinander so resultiert daraus ein Dipolmoment μ. Es hat die Einheit Cm (Coulombmeter) und ist eine vektorielle Größe, da d der Vektor zwischen den Ortskoordinaten der Punktladungen ist. Das Dipolmoment wird als Vektor oder vereinfacht als Pfeil von der negativen zur positiven Ladung geschrieben.
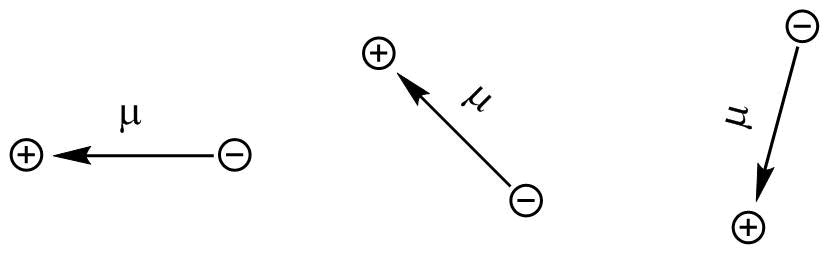
Darstellung des Dipolmoments
Dieses Prinzip lässt sich auch auf Partialladungen übertragen und ermöglicht es ein Bindungsdipolmoment zu definieren. Je größer die Elektronegativitätsdifferenz zwischen den Bindungspartnern ist, desto größer sind die resultierenden Partialladungen und das resultierende Dipolmoment der Bindung und damit ihre Polarität.
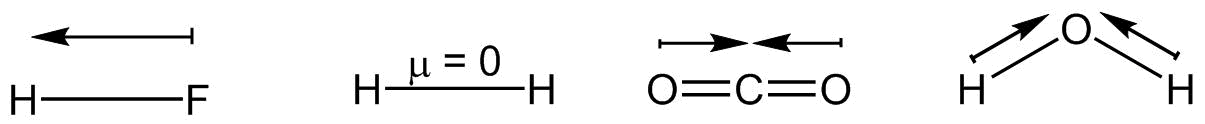
Dipolmemente verschiedener Bindungen
Mithilfe der Dipolmomente der Bindungen eines Moleküls lässt sich auch das Gesamtdipolmoment des Moleküls berechnen und damit erkennen, ob das gesamte Molekül polar oder unpolar ist. Dazu müssen alle Bindungsdipolmomente miteinander addiert werden. Das Ergebnis ist wieder ein Vektor. Ist dessen Betrag ungleich Null, so weist das Molekül ein Dipolmoment auf und ist polar. Ist dessen Betrag gleich Null, so ist das Molekül unpolar.
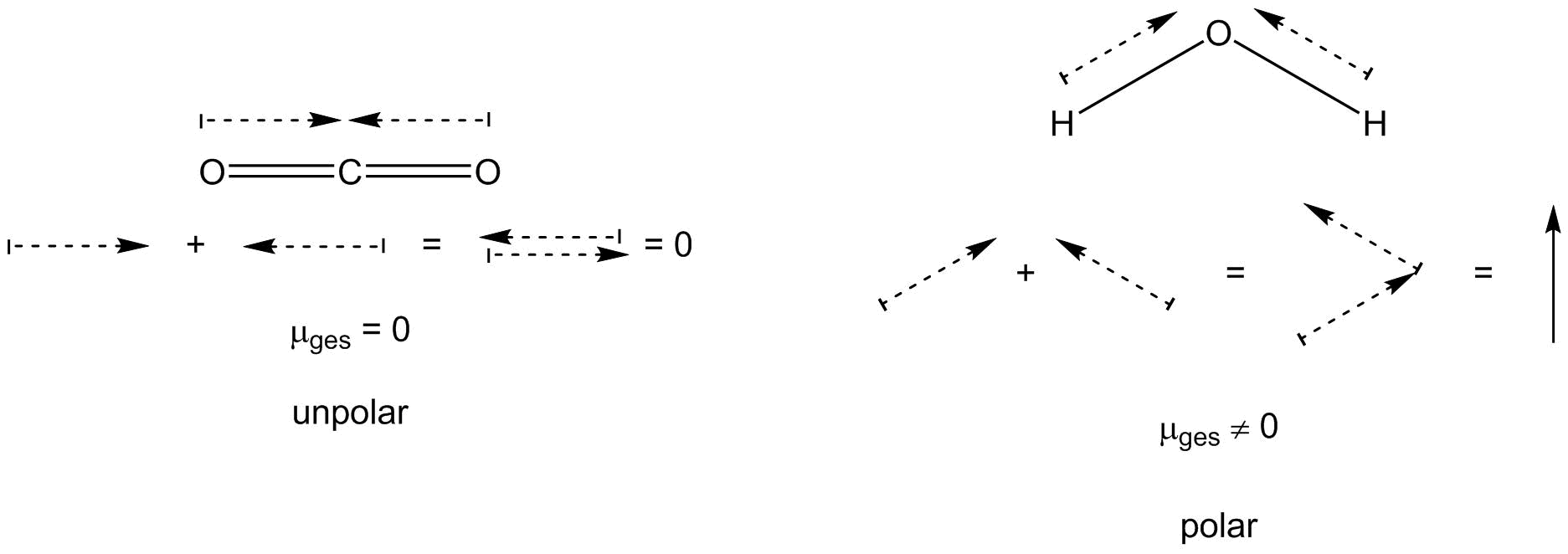
Ermittlung des Gesamtdipolmoments
Festzustellen ist, dass die Begriffe polar und unpolar relativ grob und ungenau verwendet werden. Strenggenommen ist eine Bindung nur dann unpolar, falls ihr Dipolmoment gleich Null ist. Dies ist jedoch nur der Fall, falls die Elektronegativitätsdifferenz der Bindungspartner gleich Null ist. Dies wiederum trifft nur dann zu, falls die Bindungspartner gleich, also homonuklear, sind. Festzuhalten ist, dass das Dipolmoment ein Maß für die Polarität einer Bindung oder eines ganzen Moleküls ist. Je größer das Dipolmoment, desto größer die Polarität. Bis zu welcher Größe von μ noch von unpolar und ab welcher Größe von μ von polar gesprochen wird, ist somit reine Definitionssache.
Auf der nächsten Seite wird gezeigt, wie der ionische Anteil einer Bindung abgeschätzt werden kann.
Ionischer Bindungsanteil I
Das Konzept der Elektronegativität und Partialladungen erklärt auch, weshalb die Bindungen zwischen Heteroatomen häufig stabiler sind, also eine höhere Dissoziationsenergie aufweisen, als sich aus den Dissoziationsenergien der Elemente (E AA und EBB) vorhersagen lässt. Der Grund sind elektrostatische Wechselwirkung zwischen den partialgeladenen Atomen. Die Bindungsenergie EAB der Bindung zwischen zwei Heteroatomen setzt sich folglich aus einem kovalenten und einem ionischen Anteil zusammen:
mit \( \frac{E_{AA} + E_{BB}}{2} \) kovalenter Anteil
und \( \Delta E_{AB} \) ionischer Anteil.
Sind die drei Dissoziationsenergien experimentell bestimmt worden, kann der ionische Anteil berechnet werden. Dieser wird oft auch relativ zur Bindungsenergie angegeben:
Für Fluorwasserstoff ergibt sich für den ionischen Bindungsanteil:
\[ \Delta E_{HF} = E_{HF} - \frac{E_{HH} + E_{FF}}{2} = 570 \frac{kJ}{mol} - \frac{436 \frac{kJ}{mol} + 158 \frac{kJ}{mol}}{2} = 273 \frac{kJ}{mol} \]und für den relativen ionischen Bindungsanteil:
\[ E_{AB\ relativ} = \frac{\Delta E_{AB}}{E_{AB}} = \frac{273 \frac{kJ}{mol}}{570 \frac{kJ}{mol}} = 0.48 \]Auf der nächsten Seite wird eine weitere Methode diskutiiert, den ionischen Bindungsanteil zu bestimmen.
Ionischer Bindungsanteil II
Eine weitere Möglichkeit zur Bestimmung des ionischen Anteils besteht in einem Vergleich des experimentell ermittelten Dipolmoments mit dem Dipolmoment, welches sich ergeben müsste, falls die Bindungspartner einfach entgegengesetzt geladen wären. Dazu müssen die Bindungslänge und das tatsächliche Dipolmoment bekannt sein. Beispielhaft wird dies hier am Chlorwasserstoff gezeigt:
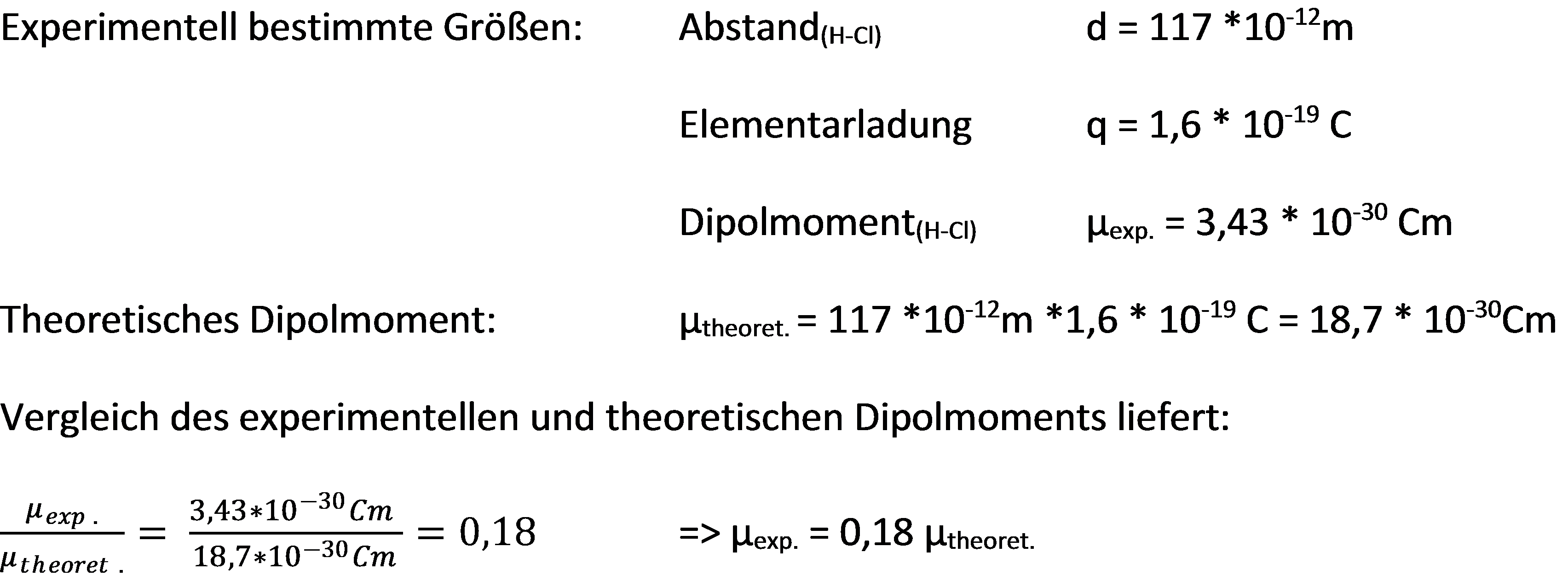
Berechnung des ionischen Bindungsanteil von HCl mithilfe des Dipolmoments
Das gemessene Dipolmoment ist 0,18-mal so groß wie das berechnete, folglich kleiner. Daraus folgt, dass die Partialladungen geringer als +1 und -1, nämlich + 0.18 und -0.18, sein müssen und damit auch der ionische Anteil der Bindung kleiner als 1, nämlich 0.18, ist.
Auf der nächsten Seite wird der Begriff Oxidationszahl eingeführt.
Oxidationszahl
Eine weitere formale Größe die mittels Kenntnis der Elektronegativität bestimmt werden kann ist die Oxidationszahl. Sie ermöglicht es zu determinieren welche Atome während einer chemischen Reaktion oxidiert und welche reduziert wurden.
Zur Ermittlung der Oxidationszahlen wird das Molekül in Valenzstrich- oder Lewisformel aufgezeichnet. Dann werden den einzelnen Atomen die vorhandenen Elektronen zugeordnet. Bei dieser Zuordnung wird wie folgt vorgegangen:
- Alle Elektronen eines Atoms, die an keiner Bindung beteiligt sind werden diesem Atom zugeordnet.
- Dann wird die Elektronegativität des betrachteten Atoms mit der Elektronegativität seines Bindungspartners verglichen. Die bindenden Elektronen werden dem Atom mit der höheren Elektronegativität zugeordnet. Dies entspricht einer heterolytischen Bindungsspaltung.
- Nun wird die Summe der einem Atom im Molekül zugeordneten Elektronen mit der Summe seiner Valenzelektronen im atomaren Zustand durch Bildung der Differenz verglichen. Die Oxidationszahl entspricht dem Wert dieser Differenz.
- In der Formel wird die Oxidationszahl dem Elementsymbol des Atoms als römische Ziffer, hochgestellt angefügt.
- Oxidationszahl = (Zahl der Valenzelektronen des freien Atoms) - (Zahl der zugeordneten Elektronen im Molekül)
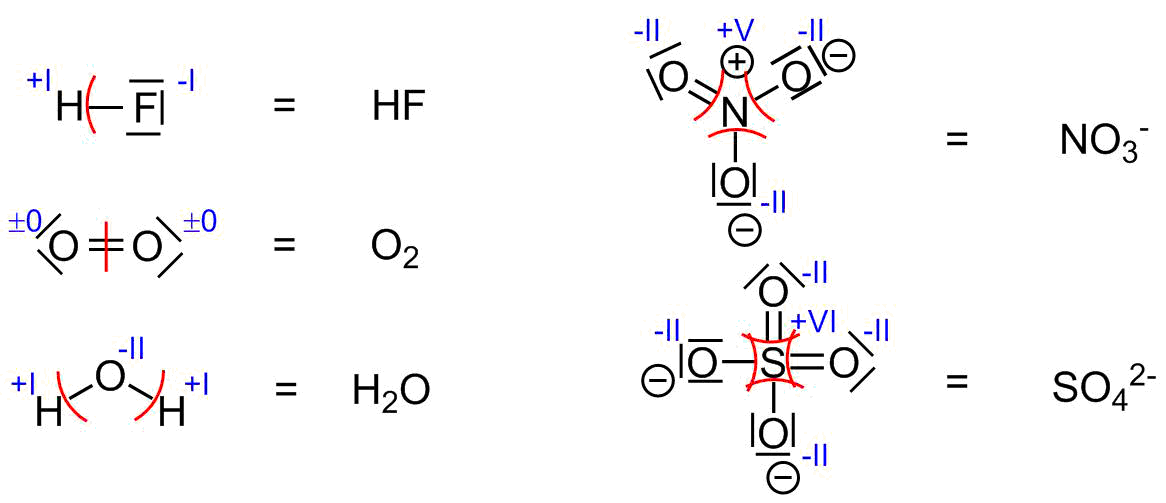
Bestimmung von Oxidationszahlen
Bei der Untersuchung der Atome hinsichtlich der Oktettregel, bei der Bestimmung
der formalen Ladung und bei der Bestimmung der Oxidationszahl werden Elektronen gezählt.
Diese Zählweisen werden auf der nächsten Seite noch einmmal verglichen.
Oktettregel, formale Ladung und Oxidationszahl
In den letzten Kapiteln haben wir die Begriffe Oktettregel, formale Ladung und Oxidationszahl kennengelernt. Diese drei Begriffe sollen hier noch einmal gegenübergestellt werden. Eine ähnlichte Tabelle, jedoch noch ohne die Oxidationszahlen, war schon im vorherigen Kapitel gezeigt.
| 1. Oktettregel | |
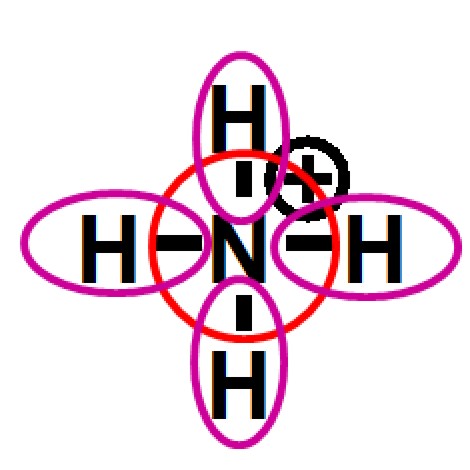
|
|
| 2. formale Ladung | |
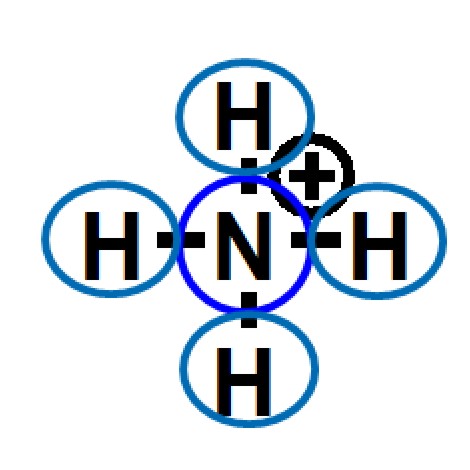
|
|
| 3. Oxidationszahl | |
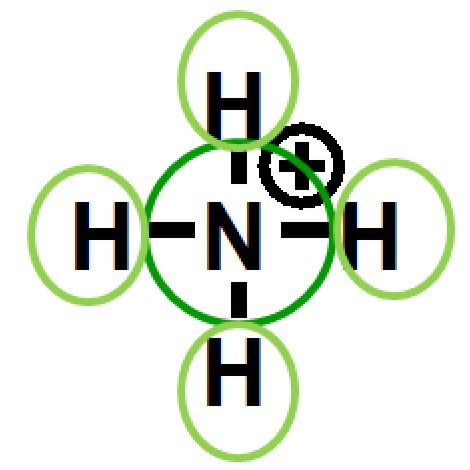
|
|
Bei der Bestimmung der Valenzelektronen im Bezug auf die Oktettregel, bei
der Bestimmung der formalen Ladung und bei der Bestimmung der Oxidationszahl
werden Elektronen gezählt. Dabei werden aber verschiedene
Vorschriften amgerwendet.
Alle drei Zählweisen sind wichtig um Moleküle
hinsichtlich ihrer chemischen Eigenschaften zu klassifizieren und
alle drei müssen gut auseinandergehalten werden.
Auf der nächsten Seite findet Ihr den Abschlusstest.
Abschlusstest
scheLM Multiple Choice
Im folgenden gibt es einen Muliple-Choice-Tests mit 15 Fragen zur Elektronegativität.
Die Tests können mehrfach bearbeitet weden. Die Fragen verändern sich. Zur Bearbeitung des Tests müsst Ihr Euch anmelden.
Im nächsten Kapitel wird der Begriff Resonanzstrukturen eingeführt.